Seguro que más de una vez hemos querido conocer la probabilidad de un hecho. Para lo que, como concepto base, deberemos saber que la probabilidad (simple) se determina dividiendo el número de ‘casos favorables’ entre el número total de ‘casos posibles’. Así, la probabilidad de que, extrayendo un numero de hasta 2 cifras (incluido el 00) éste acabe en 9 será de 1 a 10 (en realidad, 10/100). Pero, a menudo, eso de calcular el ‘total de casos posibles’, bien para calcular una probabilidad o bien, simplemente, para tener (o cifrar) el monto numérico de un hecho, requiere el conocimiento de unos conceptos estadísticos ‘en principio simples’, que son las combinaciones y las permutaciones. Y, por supuesto, conocer sus fórmulas de cálculo. Así que, hoy, vamos con ello...
PERMUTACIONES
Conocer el valor de la ‘permutación’ de N elementos tomados en grupos ‘de G en G’ significa, disponiendo de N elementos distintos, determinar cuantos posibles grupos de ‘G número de elementos’ se pueden hacer... teniendo en cuenta que importa el orden de dichos elementos dentro de cada grupo.
Esto es que si tenemos, por ejemplo, 4 elementos, A, B, C y D, el número de distintas agrupaciones de 2 elementos que se podrían formar, considerando que AB es distinto a BA, BC, distinto de CB, y distinto de AC, de AD, etc., etc.… serían las permutaciones de 4 elementos tomados de 2 en 2.
Y la formula general para calcular el número de permutaciones de N elementos tomados ‘de G en G’ es...
factorial de N dividido entre factorial de (N menos G)
(un inciso ‘para los de letras’: llamamos factorial de un número N, y se representa por ‘N!’. al resultado de multiplicar N*(N-1)*(N-2)*(N-3)… hasta llegar a *1)
Por tanto, la fórmula para calcular la permutación de N elementos tomados de G en G es…
Por tanto, la fórmula para calcular la permutación de N elementos tomados de G en G es…
P de N(G) = N!/(N-G)!
Y así, por ejemplo, si N = 4 y G =2, P4(2)= (4*3*2*1)/2*1=12
o sea, serían, en el caso...
AB, AC, AD
BA, BC, BD
CA,CB, CD
DA,DB, DC
COMBINACIONES
Hablaremos de ‘combinaciones’ cuando, con la misma idea, ahora NO importa el orden de los elementos dentro de cada grupo. Por tanto, hablamos ahora de calcular la ‘combinación de N elementos tomados de G en G’. Y es distinto porque, en este caso, y a los efectos, ABCD sería el mismo grupo que ACBD, y que BACD, que BCAD, que CBAD, que CADB, etc: Porque ‘no importa el orden, dentro del grupo’.
Y, en este caso, la fórmula matemática para calcular el número de combinaciones de N elementos tomados de G en G es...
o sea, serían, en el caso...
AB, AC, AD
BA, BC, BD
CA,CB, CD
DA,DB, DC
COMBINACIONES
Hablaremos de ‘combinaciones’ cuando, con la misma idea, ahora NO importa el orden de los elementos dentro de cada grupo. Por tanto, hablamos ahora de calcular la ‘combinación de N elementos tomados de G en G’. Y es distinto porque, en este caso, y a los efectos, ABCD sería el mismo grupo que ACBD, y que BACD, que BCAD, que CBAD, que CADB, etc: Porque ‘no importa el orden, dentro del grupo’.
Y, en este caso, la fórmula matemática para calcular el número de combinaciones de N elementos tomados de G en G es...
... factorial de N dividido entre el producto de factorial de G y factorial de (N-G)
o, puesto en anotación técnica...
C de N(G) = N!/(G!*(N-G)!)
Así que, por poner también un ejemplo, si tenemos que comer de postre dos piezas de fruta y puedes elegir entre una manzana, una pera, un plátano, una mandarina y un melocotón, sin importarte el orden, el total de posibles combinaciones (en este caso de N=5 y G=2), sería…
C de 5(2) = (5*4*3*2*1)/(2*1)*(3*2*1) = 10
O sea...
AB, AC, AD, AE
BC, BD, BE
CD, CE
DE
Pero un caso especial es cuando puede haber 'repetición' (de cada elemento de los conjuntos) (es decir, puede haber conjuntos tipo AAA, BBB, AAB, ABB, etc).
Y, en este caso...
PERMUTACIONES CON REPETICIÓN
La fórmula para calcular las Permutaciones con repetición de N elementos tomados de G en G es muy sencilla: es, simplemente... N elevado a G
C de 5(2) = (5*4*3*2*1)/(2*1)*(3*2*1) = 10
O sea...
AB, AC, AD, AE
BC, BD, BE
CD, CE
DE
Pero un caso especial es cuando puede haber 'repetición' (de cada elemento de los conjuntos) (es decir, puede haber conjuntos tipo AAA, BBB, AAB, ABB, etc).
Y, en este caso...
PERMUTACIONES CON REPETICIÓN
La fórmula para calcular las Permutaciones con repetición de N elementos tomados de G en G es muy sencilla: es, simplemente... N elevado a G
Pr de N(G) = NG
(Y así, las permutaciones con repetición de 4 elementos tomados de 2 en 2 serían 42 = 16
(¡Y de 4, tomados de tres en tres… 64…!)
COMBINACIONES CON REPETICIÓN
Por contra, en el caso de las combinaciones con repetición de N elementos tomados de G en G, la fórmula general es más compleja. Y es que tendremos que calcular previamente un número ‘M’ que es… M=N+(G-1) porque...
(¡Y de 4, tomados de tres en tres… 64…!)
COMBINACIONES CON REPETICIÓN
Por contra, en el caso de las combinaciones con repetición de N elementos tomados de G en G, la fórmula general es más compleja. Y es que tendremos que calcular previamente un número ‘M’ que es… M=N+(G-1) porque...
Las combinaciones con repetición (Cr) de N elementos tomados de G en G es igual a las combinaciones sin repetición de M elementos tomados de G en G… siendo M = N + G - 1
Cr de N(G) = C de M(G) = M!/(G!*(M-G)!)
Así que, por seguir con el ejemplo anterior, si también podríamos elegir repetir la fruta, y tomar de postre dos plátanos, o dos manzanas, (etc)... las posibilidades (combinaciones con repetición de N=5 y G=2) serían… M=5+2-1=6
y Cr de 6(2) = 6*5*4*3*2*1/(2*1)*(4*3*2*1) = 15
(Las posibles combinaciones serían las 10 que veíamos antes...mas estas cinco: AA, BB, CC, DD, EE)
O sea que la cosa se va complicando. Y aún se complicaría mucho más si se nos ocurre introducir más variantes: por ejemplo, se nos podría pedir 'cálculos condicionados', como podría ser el calcular las permutaciones de 3 elementos tomados de 14 en 14, pero con la condición de que, en cada grupo, un elemento solo pueda aparecer entre cero hasta un máximo (por poner un caso) de 7 veces…
(Esto sería una quiniela ‘reducida’, por condicionarla a que salgan, como máximo, y en cualquier posición, hasta 7 ‘unos’, o hasta 7 ‘equis’, o hasta 7 ‘doses’… y a ver qué matemático, o estadístico que se pone a hacerlo (porque si, hay una formula para ello)… cuando, a partir de ‘ya’, nos bastaría preguntárselo a ChatGPT que, en menos de 30 segundos nos dirá que hay… 2.588.496 posibles combinaciones.
O sea que este es nuestro futuro. Espero que no acabemos excesivamente ‘chatGPTdependientes…’. O, por lo menos, que sigamos sabiendo cómo se calcula una permutación ‘normal’, una combinación, el área de un triángulo… o los valores de X en las sencillas ecuaciones de segundo grado… teniendo en cuenta que para esto hay que saber extraer la raíz cuadrada.
Venga, va, por poner 'una facilita', a ver… ¿qué valores debe tener X si… X2 – 5X + 4 = 0…?
Bueee... no...
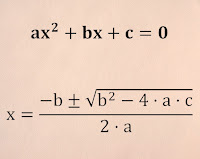
No hay comentarios:
Publicar un comentario